LeNet-5,是深度学习史上非常经典的卷积神经网络结构,由 Yann LeCun 在 1998 年提出,最初是为了解决手写数字识别问题(比如 MNIST 数据集)。它可以说是后来 CNN(包括 AlexNet、ResNet 等)的“鼻祖”。
1. LeNet-5 的基本结构
LeNet-5 由 7 层(不包括输入层)组成,包括卷积层、池化层、全连接层:
- 输入层
- 输入图像大小:32 × 32 像素灰度图。
- (MNIST 是 28 × 28,LeNet 会在周围补白到 32 × 32)。
- C1:第1个卷积层
- 卷积核大小:5 × 5
- 卷积核数量:6
- 输出特征图大小:28 × 28 × 6
- 作用:提取局部边缘、线条等低级特征。
- S2:第1个下采样层(平均池化)
- 池化核:2 × 2,步长 2
- 输出特征图大小:14 × 14 × 6
- 作用:减少参数,增强特征平移不变性。
- C3:第2个卷积层
- 卷积核大小:5 × 5
- 卷积核数量:16
- 输出特征图大小:10 × 10 × 16
- 作用:提取更复杂的形状(如角点、组合结构)。
- S4:第2个下采样层(平均池化)
- 池化核:2 × 2,步长 2
- 输出特征图大小:5 × 5 × 16
- 作用:进一步压缩特征图。
- C5:第3个卷积层(特殊,全连接卷积)
- 卷积核大小:5 × 5
- 卷积核数量:120
- 因为输入是 5 × 5,卷积后得到 1 × 1 × 120
- 作用:相当于“全连接层”,整合所有特征。
- F6:全连接层
- 节点数:84
- 使用 sigmoid 激活函数(当时没有 ReLU)。
- 作用:作为分类前的特征整合层。
- 输出层
- 节点数:10(对应 0~9 的手写数字类别)。
- 使用 Softmax 作为输出。
2. LeNet-5 的特点
- 局部连接:不同于全连接层,卷积层只和输入的一小块区域相连。
- 权值共享:同一个卷积核在不同位置共享权重,大幅减少参数数量。
- 分层特征提取:从边缘 → 局部组合 → 整体形状 → 分类结果。
- 池化机制:增强模型对位置变化的鲁棒性。
3. LeNet-5 的影响
- 是 第一个被广泛应用的卷积神经网络,在银行支票识别中取得成功。
- 奠定了现代 CNN 的基本框架(Conv → Pooling → Conv → Pooling → FC → Softmax)。
- 后续的 AlexNet (2012) 在此基础上引入了 ReLU、Dropout、GPU 训练,才真正引爆了深度学习浪潮。
那么我们如何求解卷积核中参数的梯度呢?
P1(左上): P1=ω1X1+ω2X2+ω3X4+ω4X5
P2(右上): P2=ω1X2+ω2X3+ω3X5+ω4X6
P3(左下): P3=ω1X4+ω2X5+ω3X7+ω4X8
P4(右下): P4=ω1X5+ω2X6+ω3X8+ω4X9
积核参数的梯度(反向传播)
若损失为 LLL,上游梯度记为
(k=1,2,3,4),则每个权重的梯度是“对应位置输入的加权和”:
(若有偏置 b,则 ∂L/∂b=δ1+δ2+δ3+δ4)
记忆方法:哪个输出位置用了某个权重乘了哪一个输入像素,反传时就把该输出的上游梯度乘回那像素并累加到该权重的梯度上。
推广到更大核/更大特征图/多通道完全一样:对所有位置求和即可。
降采样层(引入)
1. 为什么需要降采样层?
在卷积网络的早期设计(LeNet-5、AlexNet)里,降采样的动机主要有:
- 减少数据量:降低特征图空间尺寸,减少计算量和参数量。
- 防止过拟合:通过压缩信息,减少模型过度拟合细节噪声的风险。
- 增强平移不变性:在小范围平移、旋转下,池化能保持特征稳定(例如猫耳朵往左移一点,特征依然能被识别)。
2. 常见的降采样方式
(1) 最大池化(Max Pooling)
- 公式:从窗口内取最大值作为输出。
- 特点:保留最显著的特征,丢弃背景或弱特征。
- 常用参数:2×2 窗口,stride=2。
- 优点:效果直观,表现好。
(2) 平均池化(Average Pooling)
- 公式:对窗口内所有值取平均值。
- 特点:保留整体趋势,平滑特征。
- LeNet-5 就用了平均池化(叫“subsampling”)。
(3) 全局平均池化(Global Average Pooling, GAP)
- 公式:直接对整个特征图取平均,得到 1 个值。
- 应用:现代 CNN(如 GoogLeNet)用 GAP 来代替全连接层,减少参数并提升泛化。
(4) 随机池化 / Lp 池化
- 一些研究提出过随机选择、或者 Lp 范数池化,但应用没有前两种普遍。
通过Python来理解降采样层
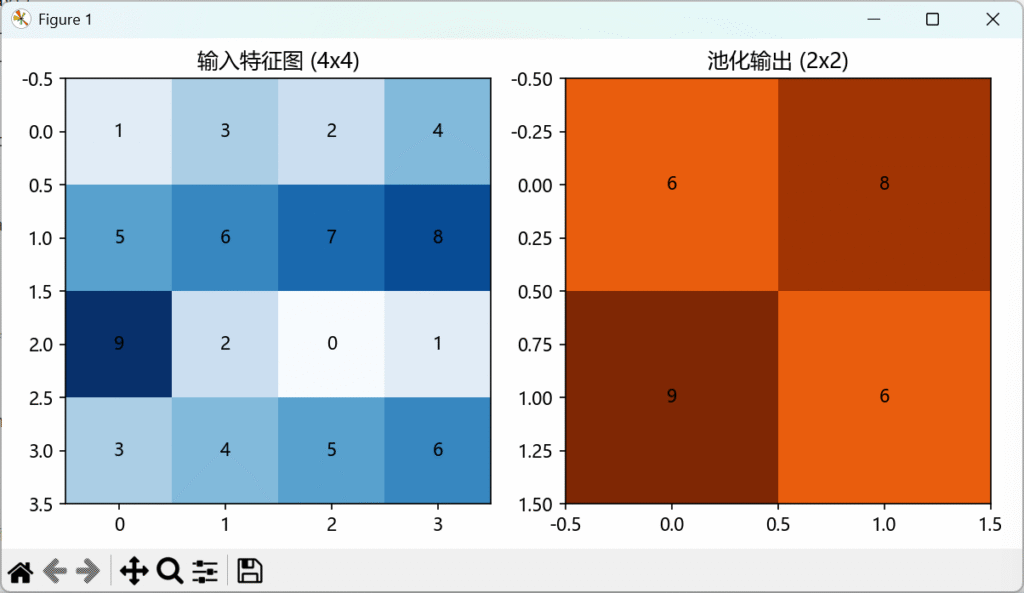
最大池化 2×2 stride=2 的图示(输入 4×4 → 输出 2×2),直观看到“降采样层”是怎么工作的
import platform
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
system = platform.system()
if system == "Windows":
matplotlib.rcParams['font.family'] = 'Microsoft YaHei'
elif system == "Darwin":
matplotlib.rcParams['font.family'] = 'Arial Unicode MS'
else:
matplotlib.rcParams['font.family'] = 'SimHei'
matplotlib.rcParams['axes.unicode_minus'] = False
# 构造一个4x4的输入特征图
input_matrix = np.array([
[1, 3, 2, 4],
[5, 6, 7, 8],
[9, 2, 0, 1],
[3, 4, 5, 6]
])
# 最大池化 2x2 stride=2
output_matrix = np.array([
[np.max(input_matrix[0:2, 0:2]), np.max(input_matrix[0:2, 2:4])],
[np.max(input_matrix[2:4, 0:2]), np.max(input_matrix[2:4, 2:4])]
])
fig, axes = plt.subplots(1, 2, figsize=(8,4))
# 输入矩阵可视化
axes[0].imshow(input_matrix, cmap="Blues", vmin=0, vmax=9)
for i in range(4):
for j in range(4):
axes[0].text(j, i, input_matrix[i,j], ha="center", va="center", color="black")
axes[0].set_title("输入特征图 (4x4)")
# 输出矩阵可视化
axes[1].imshow(output_matrix, cmap="Oranges", vmin=0, vmax=9)
for i in range(2):
for j in range(2):
axes[1].text(j, i, output_matrix[i,j], ha="center", va="center", color="black")
axes[1].set_title("池化输出 (2x2)")
plt.tight_layout()
plt.show()
效果图:
计算LeNet待估计参数个数:61684个
这个 61684 的总数,是把 C1 和 C3 不计偏置,其余层计了偏置 的“混合口径”算出来的。
逐项对应你给的公式:
- C1:5×5×6=150(只算权重,没加 6 个 bias)
- S2:0(现代实现里池化无可学习参数)
- C3:5×5×6×16=2400(只算权重,没加 16 个 bias)
- S4:0
- C5:120×(16×5×5+1)=48,120(含 bias)
- F6:120×84+84=10,164(含 bias)
- 输出:84×10+10=850(含 bias)
把这些相加:150+0+2400+0+48120+10164+850=61684
三种常见口径对齐:
| 层 | 只算权重 | 只算权重的数 | 加上偏置后的数 |
|---|---|---|---|
| C1 (5×5, in=1, out=6) | 5⋅5⋅1⋅6 | 150 | 156(+6 bias) |
| S2 (pool) | – | 0 | 0 |
| C3 (5×5, in=6, out=16,全连接) | 5⋅5⋅6⋅16 | 2400 | 2416(+16 bias) |
| S4 (pool) | – | 0 | 0 |
| C5 (5×5, in=16, out=120) | 16⋅5⋅5⋅120 | 48,000 | 48,120(+120 bias) |
| F6 (120→84) | 120⋅84 | 10,080 | 10,164(+84 bias) |
| 输出 (84→10) | 84⋅10 | 840 | 850(+10 bias) |
| 合计 | 61,470 | 61,706 |
61,684 = 上表“加上偏置”的总数 61,706 −(C1 的 6 + C3 的 16)= 61,706 − 22。
思考题请见下一页👇
微信扫描下方的二维码阅读本文

