第4章
4.用推广的Euclid算法求67mod119的逆元
解:由已知得:a=119,b=67
计算得其最大公因数为1.(见图1)
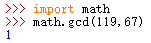
即存在一个X(X<a),使得
67X≡1mod119
有X≡67-1mod119
使用推广的欧几里得算法,有Excel公式见图2,结果见图3

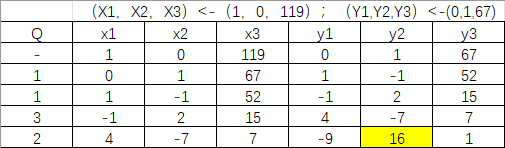
由图3得67mod119的逆元为16.
8.求25的所有本原根
解:
由已知得:n=25
有
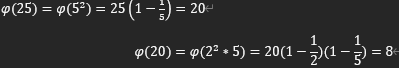
考虑2在mod9下的幂,py计算如图4所示。

整理得表1
| 底 | 幂 | mod25≡ | 结果 |
| 2 | 1 | 2 | |
| 2 | 2 | 4 | |
| 2 | 3 | 8 | |
| 2 | 4 | 16 | |
| 2 | 5 | 7 | |
| 2 | 6 | 14 | |
| 2 | 7 | 3 | |
| 2 | 8 | 6 | |
| 2 | 9 | 12 | |
| 2 | 10 | 24 | |
| 2 | 11 | 23 | |
| 2 | 12 | 21 | |
| 2 | 13 | 17 | |
| 2 | 14 | 9 | |
| 2 | 15 | 18 | |
| 2 | 16 | 11 | |
| 2 | 17 | 22 | |
| 2 | 18 | 19 | |
| 2 | 19 | 13 | |
| 2 | 20 | 1 |
有ord25(2)=y(25),可知2是25的本原根。
将结果中的质数排序,有【1,3,7,9,11,13,17,19】使用py求模数,得图5

将图5结果整理,得表2
| 底 | 幂 | mod25≡ | 结果 |
| 2 | 1 | 2 | |
| 2 | 3 | 8 | |
| 2 | 7 | 3 | |
| 2 | 9 | 12 | |
| 2 | 11 | 23 | |
| 2 | 13 | 17 | |
| 2 | 17 | 22 | |
| 2 | 19 | 23 |
将结果排序,有【2,3,8,12,13,17,22,23】,即为25的本原根
10.设通信双方使用RSA加密体制,接收方的公开钥是(e,n)=(5,35),接收到的密文是C=10,求明文M。
解:
由已知得:e=5,n=35,C=10
使用rsa加密算法有C≡memodn
将已知条件代入公式有:
10=m5mod35
使用py计算:得图6
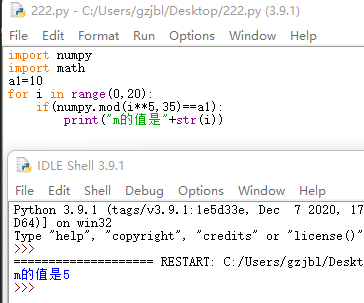
故明文M=5。
18.椭圆曲线E11(1,6)表示y2≡x3+x+6mod11,求其上的所有点。
计算有图7
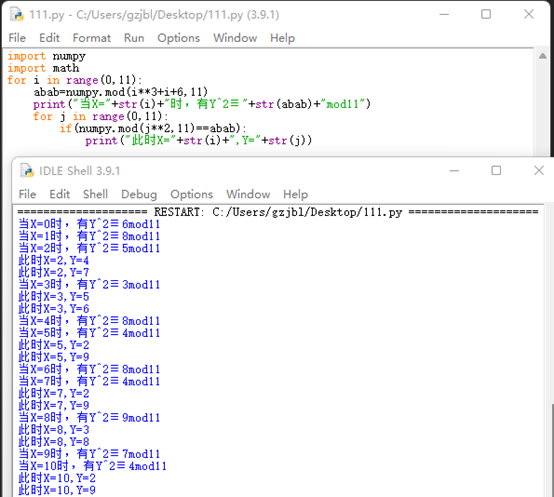
所以E11(1,6)上的所有点为(2,4)(2,7)(3,5)(3,6)(5,2)(5,9)(7,2)(7,9)(8,3)(8,8)(10,2)(10,9),O
20.利用椭圆曲线实现ELGamal密码体制,设椭圆曲线是E11(1,6),生成元G=(2,7),接收方A的秘密钥nA=7.
(1)求A的公开钥PA。
解:A的公开钥:PA=nAG=7G=2*2G+3G=(10,2)+(8,3)=(7,2)
(2)发送方B与发送消息Pm=(10,9),选择随机数k=3,求密文Cm。
C1=kG=3G=(8,3)
C2=Pm+kPA=(10,9)+3(7,2)=(10,2)
Cm={(8,3),(10,2)}
(3)显示接收方A从密文Cm恢复消息Pm的过程
Pm=C2-nAC1=Pm+kPA-nAkG=(10,2)-7(8,3)=(10,9)
微信扫描下方的二维码阅读本文

