先来回顾目前SVM的优化问题:
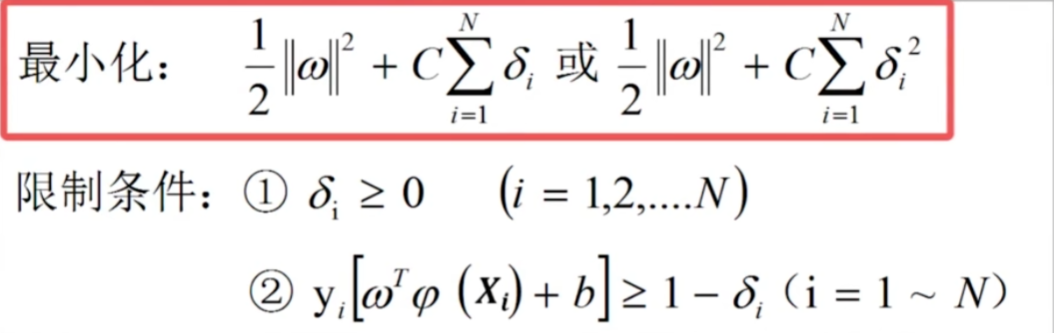
δi是slack(允许误差的大小),C是正则化参数(平衡间隔和误差)
上一讲中的限制条件:

在SVM的限制条件中yi(ωTXi+b)≥1(≥0)
需要将δi从≥0转变为:δi≤0(i=1~N).
可以得到新的目标函数:
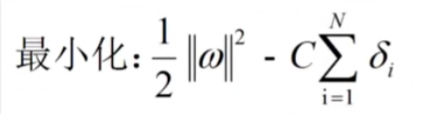
限制条件也要进行改变:
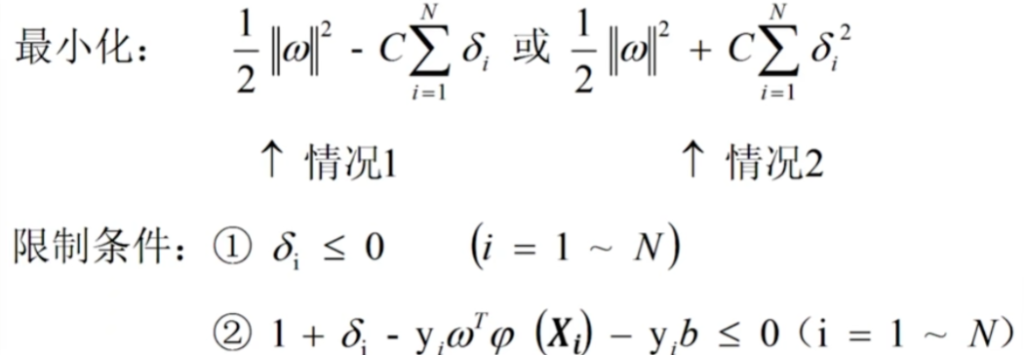
上一篇自变量ω在此处=(ω,b,δi)的组合。
gi(ω)≤0分为(1)δi≤0(i=1~N).(2)i+δi-yiωTφ(Xi)-yib≤0(i=1~N)。本篇无等式限制条件因此不存在hi(ω)≤0
将对偶问题写成如下形式:
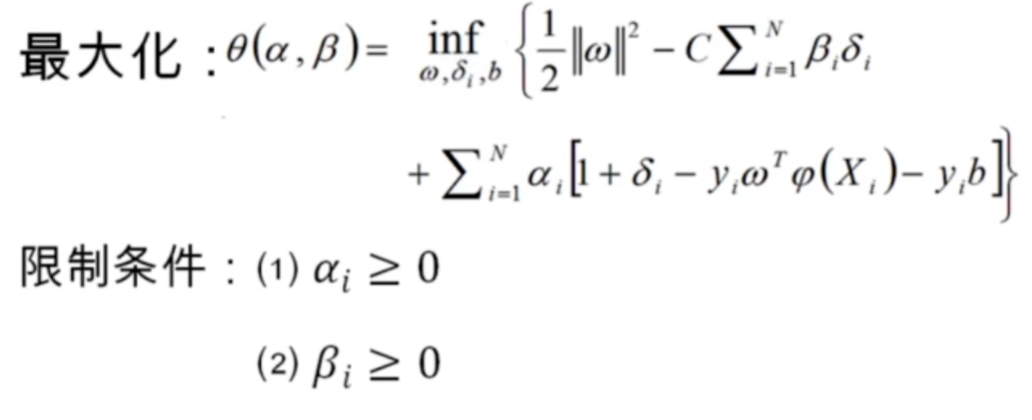
限制条件(1)(2)对应将gi(ω)≤0拆分成两个部分的条件
那么如何化为对偶问题?
对(ω,b,δi)求导并令导数为0

🟥 一条条推导图片中的三个公式:
我们知道了αi≥0是第一个约束;βi≥0是第二个约束
拉格朗日函数有:
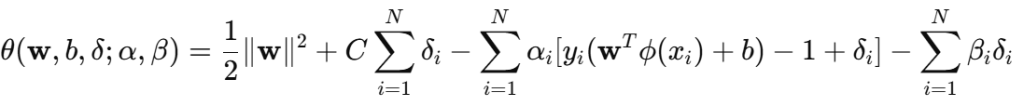
✅ (1) 对 ω 求偏导:
从上面这个 θ对ω 求偏导数:
拉格朗日中关于ω 的项有:
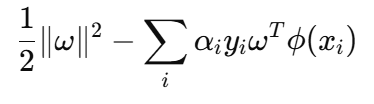
求导得:
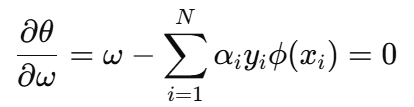
✅ 解出:
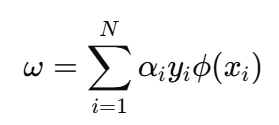
这意味着最终超平面的方向 ω 是由所有支持向量的线性组合组成的。
✅ (2) 对 δi 求偏导:
在拉格朗日中,δi 出现了三次:
- +Cδi
- - αiδi
- - βiδi
所以:
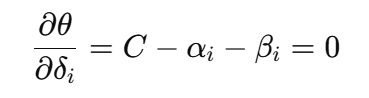
✅ 解出: αi+βi=C
这个式子揭示了软间隔下 αi 的上限约束,它不能超过 C,因为多余的惩罚会被 βi 抵消。
✅ (3) 对 b 求偏导:
b 只在 αi 项中出现,即:
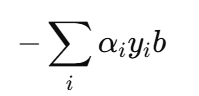
所以偏导是:
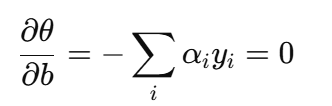
✅ 解出:
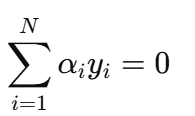
这是KKT 对偶可行性条件的一个核心结果,它限制了 αi 的线性组合,使得最终的超平面具有对称性。
🟨 总结对图片三式的解释:
| 式子编号 | 来源 | 意义 |
|---|---|---|
| (1) ω = Σαiyiφ(xi ) | 对 ω 求偏导 | 表示超平面是支持向量的线性组合 |
| (2) αi + βi=C | 对 δi 求导 | 控制 αi 不超过 C,由软间隔条件决定 |
| (3) Σαiyi = 0 | 对 b 求导 | 保证最终分界平面居中,SVM 的基本结构要求 |
微信扫描下方的二维码阅读本文

