2.7.1-原问题与对偶问题定义和KKT条件

原问题：

最小化minimize ： f(ω)

限制条件subject to: g_i(ω)≤0，i=1~k （不等式有k个）

h_i(ω)=0，i=1~m（等式有m个）

自变量ω为多维向量

定义该原问题的对偶问题如下：

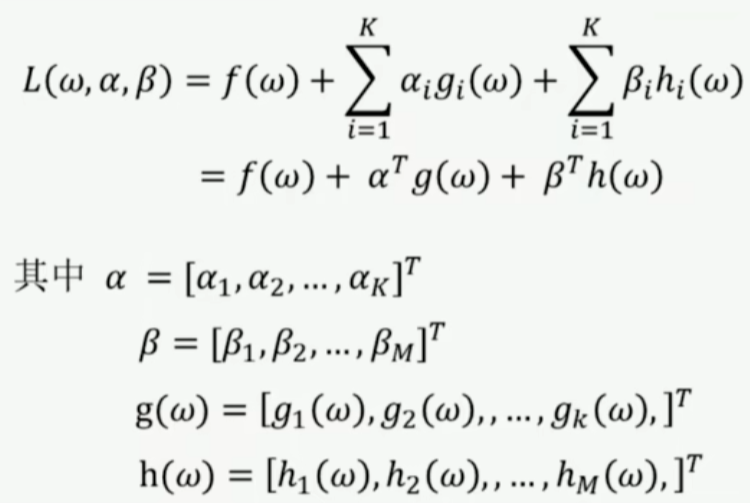
在定义了函数L（ω，α，β）基础上对偶问题如下：

【遍历定义域内所有ω找到使L（ω，α，β）最小的ω赋值为θ（α，β）】

综合得到定理1：

怎么来的？

这里我们知道有限制条件α_i≥0，本讲g_i(ω)≤0。所以α^*Tg(ω*)这一块是≤0.

h_i(ω)=0，所以β^*Th(ω*)这一块=0

那就是f(ω*)这一块加了一个≤0的α^*Tg(ω*) -->θ(α^*，β^*)≤f(ω^*)

对偶差距为f(ω^*)-θ(α^*，β^*)≥0