本讲分为两个部分。第一部分讲解梯度下降算法的具体求解过程(链式求导法);第二部分讲解更一般的神经网络(神经网络的矩阵方式)。您可根据文末分页按钮选择需要的部分阅读。
梯度下降算法的具体求解过程,或称 链式求导法
∵
∴
接着根据偏导数的链式求导法则:
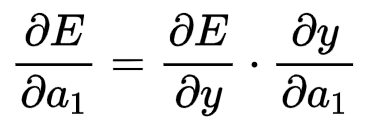
继续用链式求导法则:
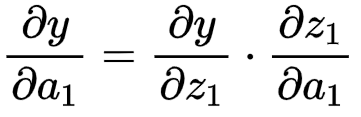
根据上式,有:
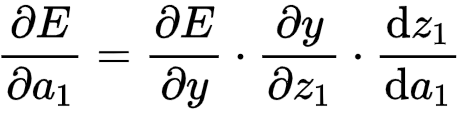
因为已经有:
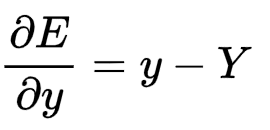
又因为y=ω1z1+ω2z2+b3
所以:
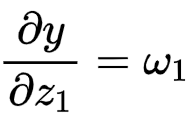
同理因为z1=φ(α1)
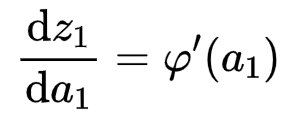
综合可得
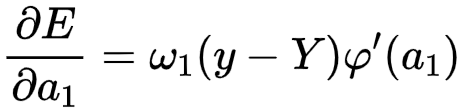
经过相似推导,有:
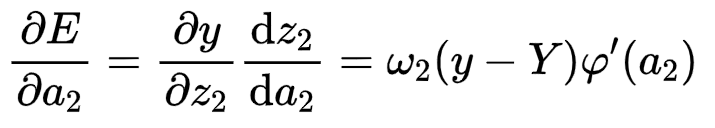
通过三个枢纽位置的偏导数求出九个偏导数:
由于:y=ω1z1+ω2z2+b3
有:
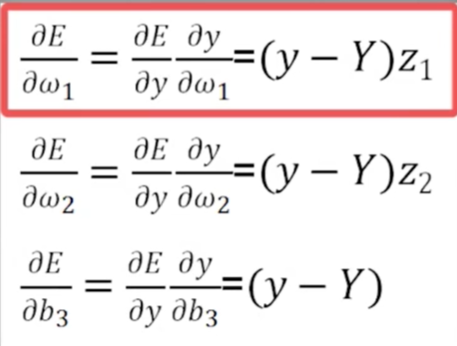
由于a1=ω11x1+ω21x2+b1
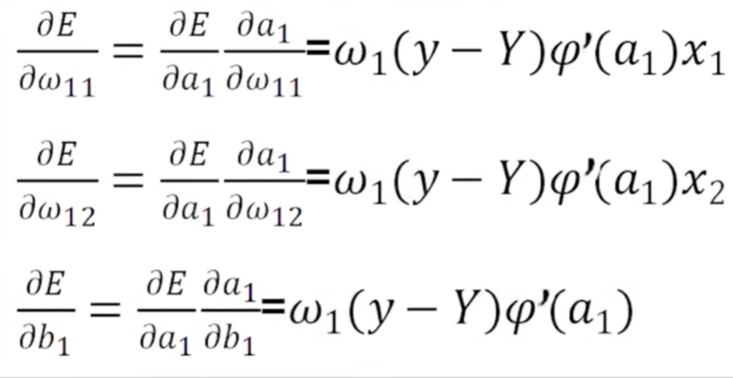
总结(第1部分)
1.对神经网络每一层各个神经元,随机选取相应的ω,b的值
2.设置目标函数E,例如E=1/2 (y-Y)2 用后向传播算法对每一个ω,b计算
3.然后用
更新ω和b的值。
4.回到2.不断循环,直到所有
很小为止,退出循环。
本部分的后向传播算法结束。请点击【第2页】来看一种更一般的神经网络👇
微信扫描下方的二维码阅读本文

1 2
