找出一个向量ω和一个常数b,使i=1......N.
(1)若yi=1,则ωTXi+b>0
(2)若yi=-1,则ωTXi+b<0
感知器树算法寻找ω,b的方法:
(1)随机选择ω,b
(2)取一个训练样本(X,Y)
- 若ωTXi+b>0,且y=-1,有ω=ω-X,b=b-1
- 若ωTXi+b<0,且y=1,有ω=ω+X,b=b+1
(3)再取另一个(X,Y),返回(2)
(4)终止条件:直到所有输入输出对(X,Y)都不满足(2)中的任一条件之一,退出循环。
⚠只要训练数据线性可分,感知器算法就一定可以停下来。

感知器算法的收敛定理

思考:现在有这个问题:如果训练数据集是线性不可分的,那么感知器算法是否还会收敛?如果此时感知器算法不收敛,能否改造这个算法,使它在线性不可分的情况下自动终止循环?
结论先行
- 标准感知器仅在数据 线性可分 时保证收敛;
- 当数据 线性不可分 时,它会“永远”更新下去(理论上更新次数无上限,实践中表现为循环或权向量爆长);
- 可以通过 Pocket 感知器、平均感知器、限步早停等改造,让算法在不可分场景下 自动终止,同时给出一个“尽可能好”的权向量。
1 为什么标准感知器不收敛?
- 更新规则 ω←ω+ηyixi, b←b+ηyi只要还存在误分类样本就持续进行。
- 线性不可分 ⇒ 任意 ω,b都有误分样本 ⇒ 条件永远满足 ⇒ 循环。
- 典型现象:权向量范数随迭代呈线性或平方根增长,错误数在一个区间内来回振荡。
2 三种常用“自动停止”改造方案
| 改造 | 思想 | 自动终止条件 | 收敛到什么 |
|---|---|---|---|
| Pocket 感知器 | 维护一份“口袋”权向量 ω*及其错误率 E*。遇到更优解就替换口袋。 | 预设 迭代上限 或 连续若干轮无改进 | 返回历史最优 ω*;即使不可分也稳定 |
| 平均感知器 | 将历次权向量求平均 ωˉ=1/T*∑[T t=1]ωt | 预设最大 epoch 数 | 理论上等价于对 hinge 损失做 SGD,泛化误差更低 |
| 限步 + 早停 | 固定最大迭代 Tmax,每轮统计误分类数;若在验证集上 N 轮不下降 则停止 | 误差“停滞” | 返回最近一次最佳 ω |
Pocket 与平均感知器都是“感知器族”中最经典、效果也最稳的两招。
2.1 Pocket 感知器核心代码片段
def pocket_perceptron(X, y, T_max=10000):
w = np.zeros(X.shape[1]); b = 0
w_best, b_best = w.copy(), b
err_best = (y*np.sign(X@w + b) <= 0).mean()
for t in range(T_max):
for i in range(len(y)):
if y[i]*(X[i]@w + b) <= 0:
w += y[i]*X[i]
b += y[i]
err_cur = (y*np.sign(X@w + b) <= 0).mean()
if err_cur < err_best:
w_best, b_best = w.copy(), b
err_best = err_cur
# 连续 10 轮没有改进就提前停
if patience_counter(err_best, t): break
return w_best, b_best
2.2 平均感知器(Averaged Perceptron)
训练时累积权向量:
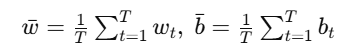
理论:等价于在所有历史超平面上做投票,可显著减小方差;在不可分数据上实验效果通常优于单一 ωt。
终止:固定 epoch 数或验证集早停。
3 其他可选策略
- 加入正则 / 损失函数替换
- 换成 平方hinge 损失+SGD ⇒ 实际就是 线性 SVM。
- 换成 logistic 损失 ⇒ 退化为 逻辑回归。
这两种都在不可分数据上天然有最优解,且一次优化即可结束。
- 核技巧
- 用核函数把数据映射到更高维,若映射后可分,感知器又可收敛;
- 但同样需 Pocket/平均方案来处理仍不可分的情况。
- 设定学习率衰减
- 令 ηt=η0/(1+t)。即使不收敛,更新幅度趋零,迭代序列 {ωt}有界 → 理论上可证明权向量收敛到一稳态值。
- 实践中常配合早停一起使用。
4 小结
- 线性不可分 ⇒ 标准感知器不收敛。
- Pocket、平均感知器、限步早停 等改造,可在给定条件下自动停止,并返回最优或平均权向量。
- 若想要“从根本上”得到凸优化解,可直接换成 SVM / Logistic 等有损失最小化目标的模型。
这样就能在任何数据分布下让“感知器思想”安全落地,而不会陷入无限循环。
微信扫描下方的二维码阅读本文

