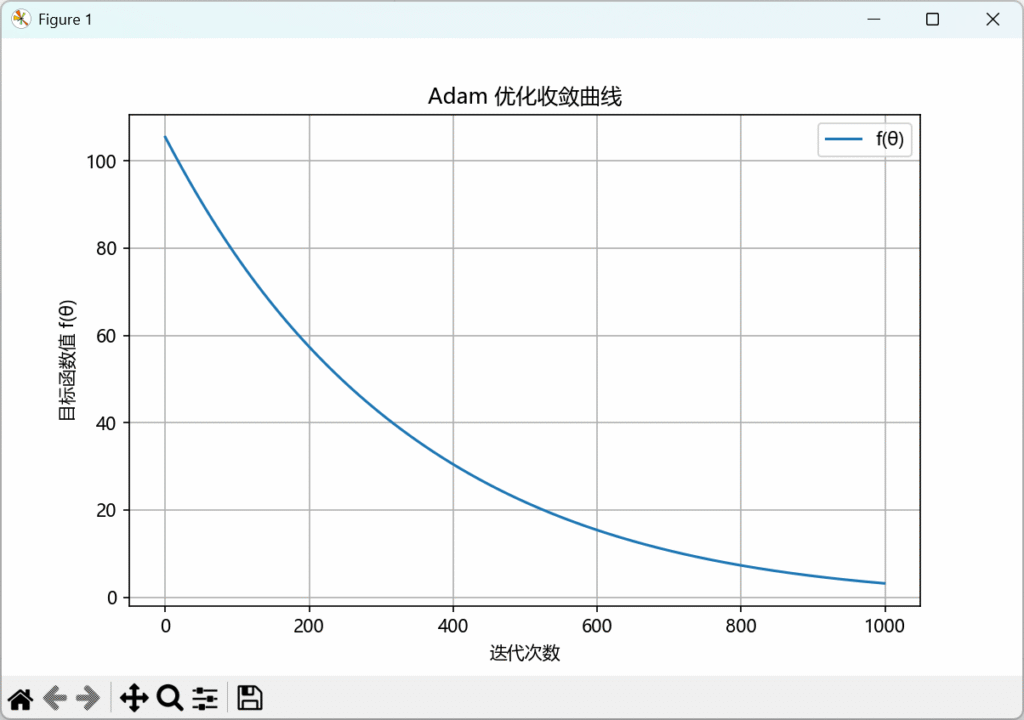
Adam 能不断减小损失函数,并逐渐收敛到最优解。
画图验证python代码:
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
import platform
system = platform.system()
if system == "Windows":
matplotlib.rcParams['font.family'] = 'Microsoft YaHei'
elif system == "Darwin":
matplotlib.rcParams['font.family'] = 'Arial Unicode MS'
else:
matplotlib.rcParams['font.family'] = 'SimHei'
matplotlib.rcParams['axes.unicode_minus'] = False
class Adam:
def __init__(self, shape, lr=1e-2, rho1=0.9, rho2=0.999, eps=1e-8):
self.lr = lr
self.rho1 = rho1
self.rho2 = rho2
self.eps = eps
self.s = np.zeros(shape)
self.r = np.zeros(shape)
self.t = 0
def step(self, theta, g):
self.t += 1
self.s = self.rho1 * self.s + (1.0 - self.rho1) * g
self.r = self.rho2 * self.r + (1.0 - self.rho2) * (g * g)
s_hat = self.s / (1.0 - self.rho1 ** self.t)
r_hat = self.r / (1.0 - self.rho2 ** self.t)
delta_theta = - self.lr * s_hat / (np.sqrt(r_hat) + self.eps)
theta = theta + delta_theta
return theta
# 模拟优化 f(θ) = ∑ θ_i^2
np.random.seed(0)
theta = np.random.randn(3) * 5.0
opt = Adam(shape=theta.shape, lr=1e-2)
losses = []
for k in range(1, 1001):
g = 2.0 * theta
theta = opt.step(theta, g)
losses.append((theta**2).sum())
# 画收敛曲线
plt.figure(figsize=(8,5))
plt.plot(losses, label="f(θ)")
plt.xlabel("迭代次数")
plt.ylabel("目标函数值 f(θ)")
plt.title("Adam 优化收敛曲线")
plt.legend()
plt.grid(True)
plt.show()
微信扫描下方的二维码阅读本文

1 2
