🟩 一、KKT 条件是什么?
KKT 条件是求解带约束优化问题的“最佳通用工具”。
它是拉格朗日乘子法的扩展,可以处理不等式约束。
用学过的内容理解:若f(ω*)=θ(α*,β*),则通过上一篇的定理一推出:对于所有的i=1~k,要么αi=0,要么gi(ω*)=0。这就是KKT条件
🟦 二、复习原问题长什么样?
还记得 SVM 的原问题是:
最小化:
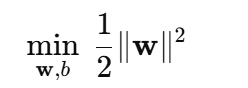
约束条件(对每个样本 i):
yi(ωTXi+b)≥1
我们记这个约束为: gi(ω,b)=1−yi(ωTXi+b)≤0
🟥 三、KKT 条件的四大要点
KKT 条件分四个部分,适用于最小化问题:
1️⃣ 原始可行性(Primal Feasibility):
必须满足原问题的约束: yi(ωTXi+b)≥1⇒gi(ω,b)≤0
2️⃣ 对偶可行性(Dual Feasibility):
拉格朗日乘子 αi > 0(不能为负)
3️⃣ 互补松弛条件(Complementary Slackness):
这是 SVM 中最重要的一条: αi⋅gi(ω,b)=0
也就是说:
- 如果某个点不在边界上(分类边界之外),那么它的 αi= 0(不是支持向量)
- 如果某个点在“刚好边界上”,即 gi(·)= 0$,那么它的 αi > 0(是支持向量)
这就是支持向量名字的来源!
4️⃣ 梯度零条件(Stationarity):
这是说原函数 + 拉格朗日项对变量的导数要为 0:
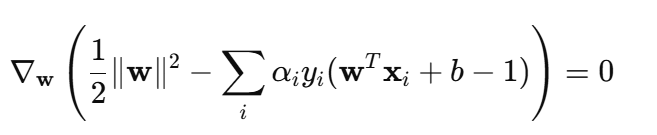
计算导数会发现:
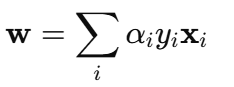
这说明权重 ω 可以由支持向量加权组成!(这也是 SVM 只依赖支持向量的根本原因)
🟨 四、KKT 条件的作用是?
| 作用 | 说明 |
|---|---|
| ✅ 判断最优 | 满足 KKT 条件就说明找到了最优解(对于凸问题,如 SVM) |
| ✅ 找支持向量 | 哪些点是支持向量,直接看哪几个 αi > 0 |
| ✅ 构建对偶问题 | 推导对偶形式的基础 |
| ✅ 核函数通道 | 对偶问题只出现 α 和点积 → 可以用核函数代替 |
📌 总结一句话:
🎯 KKT 条件是支持向量机最优解的必要条件,
它揭示了哪些点是支持向量,解释了 ω 怎么由 α 决定,
并且它让我们能把原问题完美转化为对偶问题。
微信扫描下方的二维码阅读本文

