🟥 1. 什么是原问题?
我们在 SVM 中最开始要解决的是这个问题:
🎯 原始目标:找一条最优分类直线,让间隔最大
我们把它写成优化形式:
原问题(Primal Problem):
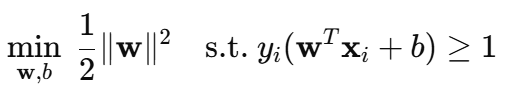
解释一下这公式的意思:
- ω 是直线的方向
- b 是直线偏移量
- 我们要让分类结果 yi 和( ωTXi+ b) 一致,并且距离至少是 1
🟩 2. 什么是对偶问题?
原问题中变量是 (ω, b),但它不好直接解,尤其在引入核函数时非常麻烦。
我们可以用一种方法把它变成另一个数学形式,叫做“对偶问题(Dual Problem)”,它是:
对偶问题:
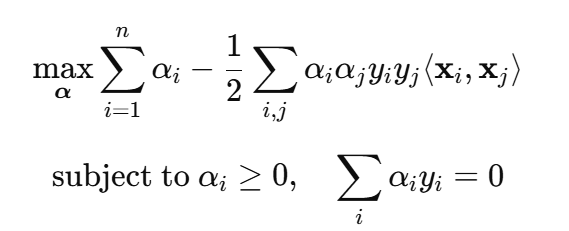
这里的变量是 αi,叫做“拉格朗日乘子”(你可以理解为每个样本点的“影响因子”)。
🟦 3. 为什么要构造对偶问题?有什么好处?
| 原问题 | 对偶问题 |
|---|---|
| 变量是 ω, b | 变量是 αi |
| 必须显式处理 Xi | 只出现点积 <Xi,Xj> |
| 不能轻易引入核函数 | 能直接用核函数替代点积 |
✅ 对偶问题最大好处:可以引入核函数 K(x, x')
当我们用非线性变换时,只要把 <Xi,Xj> 换成 K(Xi, Xj),就可以进行核 SVM 计算!
🟨 4. 原问题与对偶问题的关系(总结)
- 原问题是直观定义,目标是最小化 ||ω||2
- 对偶问题是通过“拉格朗日对偶性”从原问题推导出来的等价形式
- 原问题里我们直接优化 ω,但不好用在非线性空间
- 对偶问题则可以轻松引入核函数,处理高维甚至无限维空间
- 对偶问题解出的 αi 可以用来重建 ω 和分类函数
📌 一句话总结:
原问题是我们要解决的实际几何问题,
对偶问题是换一种方式解这个问题,让它变得更容易、更强大,尤其是可以引入核函数处理非线性数据。
微信扫描下方的二维码阅读本文

