问题:如下图所示,这是一个线性不可分的情况。因为x把o给包围起来了。我们找不到一条合适的直线将x和o完全分开。那么我们需要怎么做才可以将这个线性不可分的情况变成线性可分的情况呢?
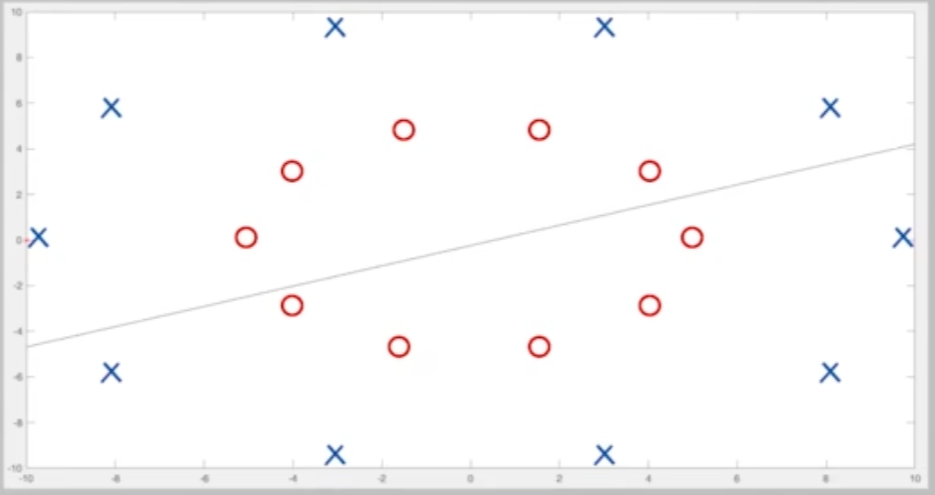
✅ 抛出问题:SVM 该怎么办?
支持向量机(SVM)默认找一条线性分隔超平面。但这个图中明显做不到。怎么办呢?
我们有两个解决方向:
1️⃣ 使用 核函数 SVM(Kernel SVM)
将原始的二维数据(X1,X2)映射到高维空间,比如:
ϕ(X1,X2)=(X1,X2,X12+X22)
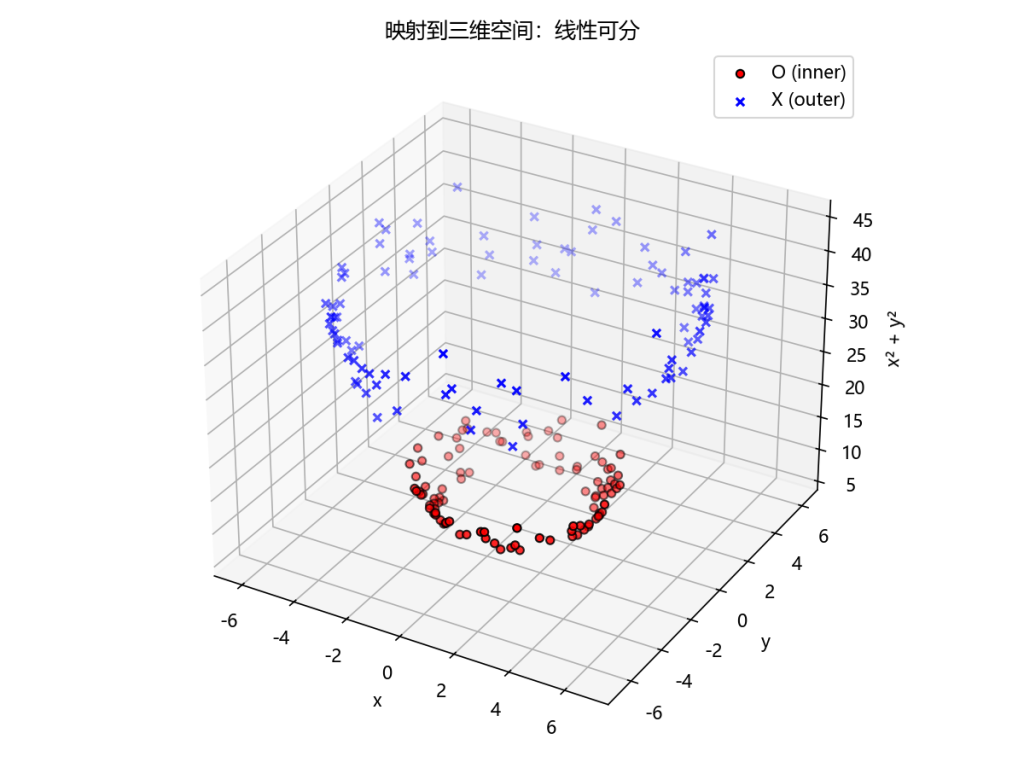
在新空间中,距离原点近的点(O)和远的点(X)可以用一个平面分开。这个方法就可以处理这类“圆环结构”的数据。
效果图像: 变换后可以在高维中画一个平面,等价于在原始二维平面中画一个“圆形决策边界”。
2️⃣ 或者使用 RBF 核(径向基核)
K(X,X′)=exp(−γ||X−X′||2)
RBF 核可以隐式地把数据映射到无限维空间,从而实现非线性分割,这类“内外包围结构”对 RBF 核非常友好。
🟦 二、想法:变换空间!
核心思想:在当前空间分不开,那我们就把它“变形”一下,在一个新的空间中试试看!
这就引出了两个大招:
✅ 方法1:手动设计“特征映射” φ(x)
我们先举个经典例子。
假设你的输入是二维的 (X1, X2)
可以设计一个新的第三个维度: z=X12+X22
这样我们就把每个点 (X1,X2) 映射到了三维空间:ϕ(X1,X2)=(X1,X2,X12+X22)
在这个新空间里:
- 所有红圈“O”点的 X12+X22 比较小(靠近原点)
- 所有蓝叉“X”点的 X12+X22比较大(离得远)
现在,我们可以用一个“平面”来分开这两类点!
✅ 在三维空间里可分 ⇒ 就相当于我们“非线性地”把数据在二维里分开了。
也可以放松限制条件--》对每个训练样本和标签(Xi+Xi)设置松弛变量δi,即有yi(ωTXi+b)≥1-δi,∀i
设置新的约束:

✅ 方法2:用核函数(Kernel Trick)
核函数的本质就是:
用一种数学方式,让我们“好像”把数据映射到高维空间去分开它们,但实际上不用真的算高维的坐标。
比如可以用RBF 核函数: K(X,X′)=exp(−γ||X−X′||2)
这个核能处理“同心圆”“包围结构”“斑点状”的数据。
你不用写 ϕ(X)映射,也不用写 z=X12+X22,直接调用核函数就行。
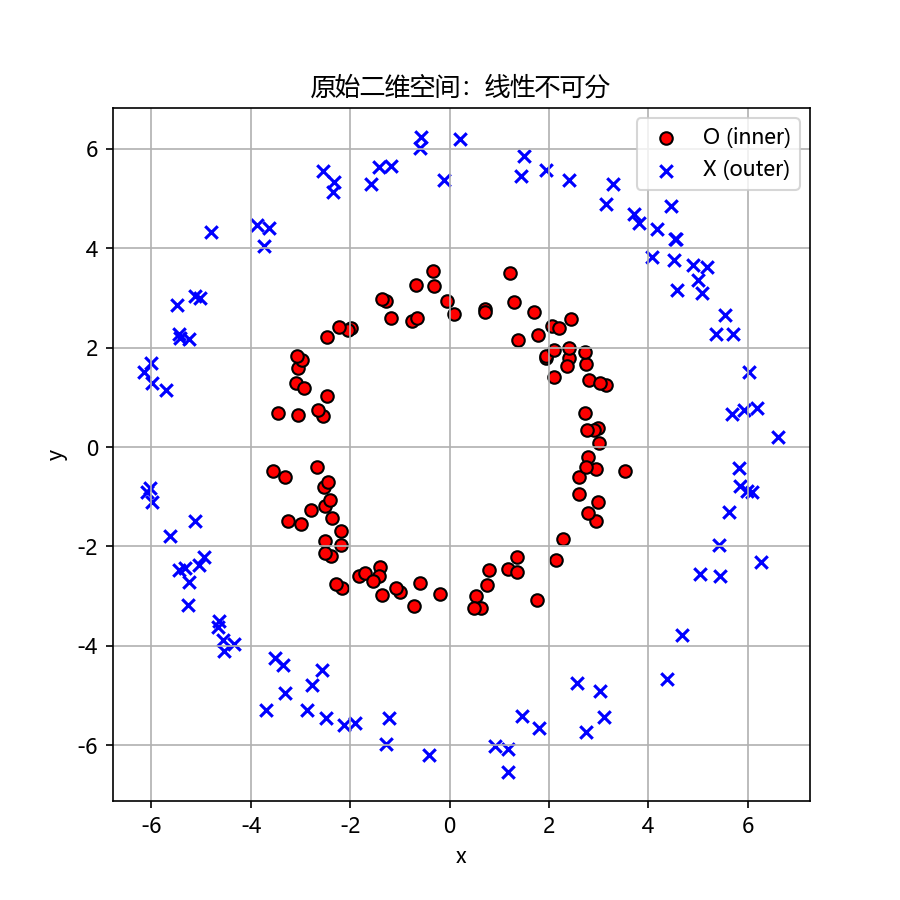
🟥 三、图像理解
在图里:
- “O” 是内圈,距离原点近
- “X” 是外圈,距离原点远
如果用 r = X12+X22 这个新维度:
| 原空间 | 新空间 (X1,X2,r) |
|---|---|
| O 点集中在小 r 位置 | 距离原点近 → 新轴方向靠“下” |
| X 点集中在大 r 位置 | 离原点远 → 新轴方向靠“上” |
| 原空间不可线性分 | 新空间可用“平面”线性分 → 成功! |
🟨 四、最终目的:让数据变成线性可分
| 方法 | 做了什么 | 优点 |
|---|---|---|
| 特征映射 | 手动添加新维度,比如 X2+Y2 | 直观好理解 |
| 核函数(SVM) | 隐式变换数据,不用手动写高维特征 | 自动化、适用更复杂结构 |
✅ 小结
🎯 当数据线性不可分,我们可以用特征映射或核函数把数据“抬到更高的空间”,让它变成线性可分,从而让 SVM 找到完美的分类超平面。
✅用Python来进行演示:
💡代码:
💡效果:
微信扫描下方的二维码阅读本文

