2.2课后思考-线性可分条件下的数学推导证明满足条件的分类超平面唯一

我们知道支持向量机寻找的最优分类应当满足以下三个条件：1.该直线分开了两类，2.该直线最大化间隔margin，3.该直线处于间隔中间，到所有支持向量机的距离相等。
那么是否可以用严格的数学证明：在线性可分条件下，有且只有一条直线满足上面的三个条件呢？

1.优化问题的形式
在实用推导中，将间隔问题等价地转为凸二次优化问题（Hard‑Margin SVM）：

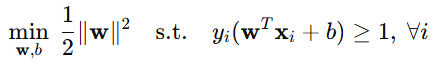
该目标函数是 严格凸的（因为是 |w|²），约束条件是线性的，因此构成一个 严格凸优化问题。
严格凸＋线性约束 ⇒ 唯一解

2.严格凸性导致唯一性
严格凸函数在凸可行域内只能有一个全局最小点（最优解）。这里的 Hessian 正定，从而保证唯一性

3.几何直观解释
虽然在纯“线性可分”前提下，确实存在无限多条分隔直线（可以随意平移、倾斜），但最大化间隔的这一附加条件只允许一个最优解。
换句话说，在所有能正确分类的解中，只有一条超平面能使到两类最近点（支持向量）的间隔最大

在数据严格线性可分的条件下，Hard‑Margin SVM 的优化问题是一个严格凸的二次规划问题，因此其最优解 —— 即满足“分隔+最大化间隔且位于中间”的那条超平面 —— 是全局唯一。

如果数据允许软间隔（slack 变量），问题仍为凸，但可能不严格凸，从而不一定保证唯一解（尤其在某些边界配置下）【参考文献】：GeeksforGeeks+1计算机科学系+1。
在奇异配置下（如支持向量数量超过数据维度+1），虽然解仍唯一，但支持向量组合可能不唯一【参考文献】：计算机科学系+4ece.iisc.ac.in+4NeurIPS 论文集+4。

结论：

在“硬间隔线性可分”前提下，只存在一条满足“三大条件”的最优分隔直线。用严格凸性 + 一阶最优/二阶条件结合可以严格证明其唯一性。