📌单纯用识别率判断系统的性能好坏是没有意义的。
这时候就需要用到混淆矩阵:
| 预测 | 正向 | 负向 | |||
| 实 | 正向 | TP | + | FN | =1 |
| 际 | 负向 | FP | + | TN | =1 |
TP:正向识别为正向结果
FN:正向识别为负向结果
FP:负向识别为正向结果
TN:负向识别为负向结果。
可以看到只有TP,TN是期望的情形。因为他们把实际的东西正确识别到了。
容易得到瞎猜的概率: (FP+FN)/(TP+TN+FP+FN)
TPR(真正率 / Recall) TPR=TP/(TP+FN)
FPR(假正率) FPR=FP/(FP+TN)
引入概念:ROC曲线
对于同一个系统来说,如果TP增加,那么FP也会随之增加
直观的理解:
对于同一个系统,如果我们把更多的正样本识别为正样本,那么我们也会把更多的负样本识别为正样本。
得到如下关系:
FN减少--TP增加--FP增加--TP减少
人为改变阈值:TP和FP同时增减。
如果系统性能更好:从算法本身来弄(即设计更好的算法)
📊 理解 ROC 图的意义
- 理想分类器:
- ROC 曲线快速上升到左上角
- AUC(曲线下面积)接近 1.0
- 完全随机猜测:
- ROC 曲线是对角线 y=x
- AUC = 0.5
- 糟糕分类器:
- ROC 曲线在对角线下方(说明预测反着来还更准)
📊怎么画ROC曲线
0.对每个测试样本计算如图2.13.1-1 的值
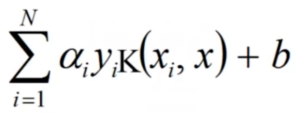
1.将0步的计算结果从小到大排序
2.计算此时的TP,FP
3.将每个值作为一个阈值
4.连成一条曲线
在3.中:你可以不断调整判断阈值(比如从 0 到 1):
- 阈值低:很多样本会被判为正类 ⇒ TPR ↑ 但 FPR ↑
- 阈值高:更严格,只有高分样本被判为正类 ⇒ TPR ↓ FPR ↓
每个阈值对应一对 (FPR, TPR),在平面上就是一个点
曲线下面积AUC:是曲线右下角的面积大小(面积越大越好)
等错误率EER:从左上-右下对角连线,形成与ROC曲线的交点,与X轴作垂线,垂线的X值越小越好。
画兵王问题Matlab程序的ROC曲线代码:
import scipy.io as sio
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
import numpy as np
# 加载新的 MATLAB 文件
mat = sio.loadmat("/mnt/data/svm_results.mat")
# 提取变量
y_true = mat['yTesting'].ravel()
decision_values = mat['decisionValues'].ravel()
# 若标签为 -1/1 转为 0/1
if set(np.unique(y_true)) == {-1, 1}:
y_true = (y_true + 1) // 2 # -1 -> 0, 1 -> 1
# 计算 ROC 曲线和 AUC
fpr, tpr, thresholds = roc_curve(y_true, decision_values)
roc_auc = auc(fpr, tpr)
# 计算 EER
fnr = 1 - tpr
eer_index = np.nanargmin(np.abs(fpr - fnr))
eer = (fpr[eer_index] + fnr[eer_index]) / 2
# 绘图
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, label=f'ROC Curve (AUC = {roc_auc:.4f})', color='blue')
plt.plot([0, 1], [0, 1], 'k--', label='Random Guess')
plt.plot(fpr[eer_index], tpr[eer_index], 'ro', label=f'EER = {eer:.4f}')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve from MATLAB SVM Output')
plt.legend(loc='lower right')
plt.grid(True)
plt.tight_layout()
plt.show()🚩代码运行如图2.13.1-2所示
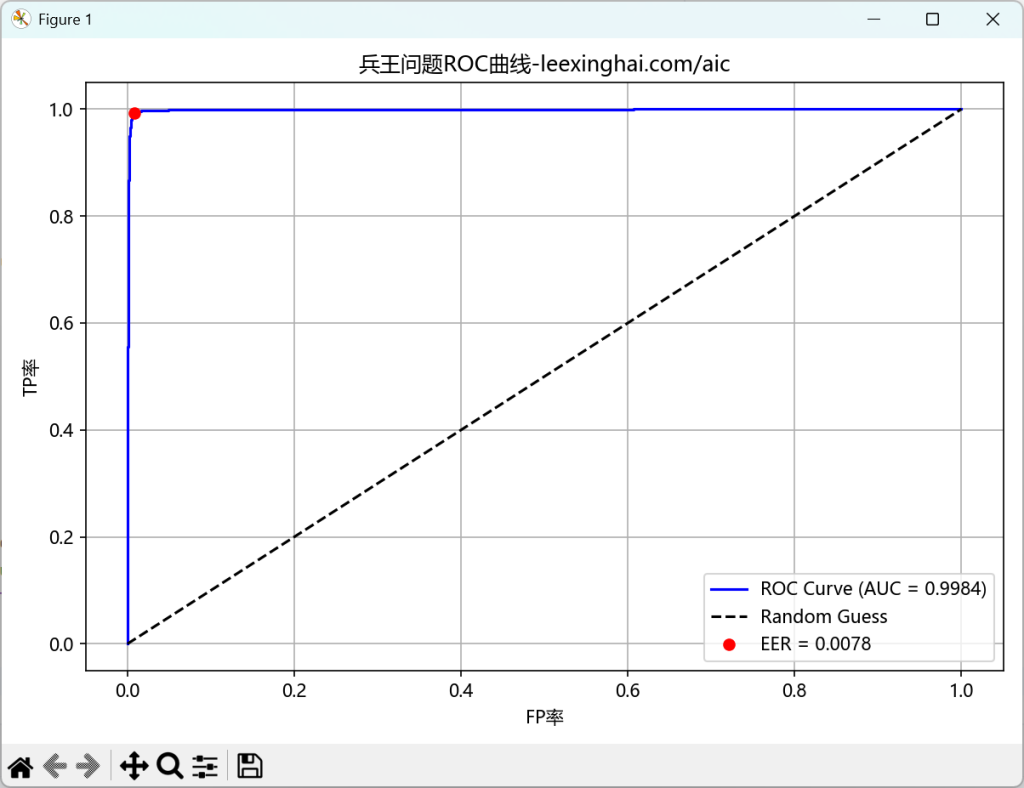
可知:
AUC=0.9984(曲线右下角的面积)
等错误率EER=0.0078(点在X轴的值)
微信扫描下方的二维码阅读本文

